Algorithms For Generating Private Key
- Algorithms For Generating Private Key Finder
- Private Key Algorithm
- Algorithms For Generating Private Key West
- Algorithms For Generating Private Key Example
- Sudoku Generating Algorithm
- Algorithms For Generating Private Keyboard
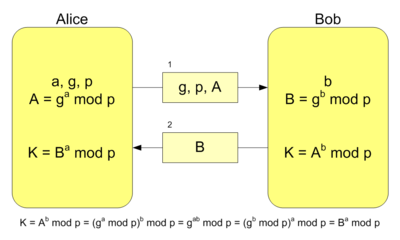
Creating and managing keys is an important part of the cryptographic process. Symmetric algorithms require the creation of a key and an initialization vector (IV). The key must be kept secret from anyone who should not decrypt your data. The IV does not have to be secret, but should be changed for each session. Asymmetric algorithms require the creation of a public key and a private key. The public key can be made public to anyone, while the private key must known only by the party who will decrypt the data encrypted with the public key. This section describes how to generate and manage keys for both symmetric and asymmetric algorithms.
Symmetric Keys
The symmetric encryption classes supplied by the .NET Framework require a key and a new initialization vector (IV) to encrypt and decrypt data. Whenever you create a new instance of one of the managed symmetric cryptographic classes using the parameterless constructor, a new key and IV are automatically created. Anyone that you allow to decrypt your data must possess the same key and IV and use the same algorithm. Generally, a new key and IV should be created for every session, and neither the key nor IV should be stored for use in a later session.
- Oct 09, 2019 How to Generate & Use Private Keys using OpenSSL's Command Line Tool. These commands generate and use private keys in unencrypted binary (not Base64 “PEM”) PKCS#8 format. The PKCS#8 format is used here because it is the most interoperable format when dealing with software that isn't based on OpenSSL.
- Mar 28, 2019 It is used in elliptic curve cryptography as a means of producing a one-way function, which is a function that is easy to compute in one direction, but difficult to do so in the opposite direction. In cryptocurrency systems such as Bitcoin, this one-way function takes the private key as an input to generate the public key, which is the output.
To communicate a symmetric key and IV to a remote party, you would usually encrypt the symmetric key by using asymmetric encryption. Sending the key across an insecure network without encrypting it is unsafe, because anyone who intercepts the key and IV can then decrypt your data. For more information about exchanging data by using encryption, see Creating a Cryptographic Scheme.
So when you encode a public or private key into bytes (so that they may be stored in a file), you will need more than just the bytes for the modulus. A 2048-bit modulus can theoretically fit over exactly 256 bytes (since 256.8 = 2048) but you need more bytes to encode the other values. Public-key algorithms use a public key and a private key. The public key is made available to anyone (often by means of a digital certificate ). A sender encrypts data with the receiver's public key; only the holder of the private key can decrypt this data. Asymmetric algorithms require the creation of a public key and a private key. The public key can be made public to anyone, while the private key must known only by the party who will decrypt the data encrypted with the public key. This section describes how to generate and manage keys for both symmetric and asymmetric algorithms. Symmetric Keys.
The following example shows the creation of a new instance of the TripleDESCryptoServiceProvider class that implements the TripleDES algorithm.
When the previous code is executed, a new key and IV are generated and placed in the Key and IV properties, respectively.
Sometimes you might need to generate multiple keys. In this situation, you can create a new instance of a class that implements a symmetric algorithm and then create a new key and IV by calling the GenerateKey and GenerateIV methods. The following code example illustrates how to create new keys and IVs after a new instance of the symmetric cryptographic class has been made.
When the previous code is executed, a key and IV are generated when the new instance of TripleDESCryptoServiceProvider is made. Another key and IV are created when the GenerateKey and GenerateIV methods are called.
Asymmetric Keys
Algorithms For Generating Private Key Finder
The .NET Framework provides the RSACryptoServiceProvider and DSACryptoServiceProvider classes for asymmetric encryption. These classes create a public/private key pair when you use the parameterless constructor to create a new instance. Asymmetric keys can be either stored for use in multiple sessions or generated for one session only. While the public key can be made generally available, the private key should be closely guarded.
A public/private key pair is generated whenever a new instance of an asymmetric algorithm class is created. After a new instance of the class is created, the key information can be extracted using one of two methods:
The ToXmlString method, which returns an XML representation of the key information.
The ExportParameters method, which returns an RSAParameters structure that holds the key information.
Both methods accept a Boolean value that indicates whether to return only the public key information or to return both the public-key and the private-key information. An RSACryptoServiceProvider class can be initialized to the value of an RSAParameters structure by using the ImportParameters method.
Asymmetric private keys should never be stored verbatim or in plain text on the local computer. If you need to store a private key, you should use a key container. For more on how to store a private key in a key container, see How to: Store Asymmetric Keys in a Key Container.
The following code example creates a new instance of the RSACryptoServiceProvider class, creating a public/private key pair, and saves the public key information to an RSAParameters structure.
See also
In cryptocurrencies, a private key allows a user to gain access to their wallet. The person who holds the private key fully controls the coins in that wallet. For this reason, you should keep it secret. And if you really want to generate the key yourself, it makes sense to generate it in a secure way.
Idm 6.25 key generator. Here, I will provide an introduction to private keys and show you how you can generate your own key using various cryptographic functions. I will provide a description of the algorithm and the code in Python.
Do I need to generate a private key?

Most of the time you don’t. For example, if you use a web wallet like Coinbase or Blockchain.info, they create and manage the private key for you. It’s the same for exchanges.
Mobile and desktop wallets usually also generate a private key for you, although they might have the option to create a wallet from your own private key.
So why generate it anyway? Here are the reasons that I have:
- You want to make sure that no one knows the key
- You just want to learn more about cryptography and random number generation (RNG)
What exactly is a private key?
Formally, a private key for Bitcoin (and many other cryptocurrencies) is a series of 32 bytes. Now, there are many ways to record these bytes. It can be a string of 256 ones and zeros (32 * 8 = 256) or 100 dice rolls. It can be a binary string, Base64 string, a WIF key, mnemonic phrase, or finally, a hex string. For our purposes, we will use a 64 character long hex string.
Why exactly 32 bytes? Great question! You see, to create a public key from a private one, Bitcoin uses the ECDSA, or Elliptic Curve Digital Signature Algorithm. More specifically, it uses one particular curve called secp256k1.
Now, this curve has an order of 256 bits, takes 256 bits as input, and outputs 256-bit integers. And 256 bits is exactly 32 bytes. So, to put it another way, we need 32 bytes of data to feed to this curve algorithm.
There is an additional requirement for the private key. Because we use ECDSA, the key should be positive and should be less than the order of the curve. The order of secp256k1 is FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141, which is pretty big: almost any 32-byte number will be smaller than it.
Naive method
So, how do we generate a 32-byte integer? The first thing that comes to mind is to just use an RNG library in your language of choice. Python even provides a cute way of generating just enough bits:
Looks good, but actually, it’s not. You see, normal RNG libraries are not intended for cryptography, as they are not very secure. They generate numbers based on a seed, and by default, the seed is the current time. That way, if you know approximately when I generated the bits above, all you need to do is brute-force a few variants.
When you generate a private key, you want to be extremely secure. Remember, if anyone learns the private key, they can easily steal all the coins from the corresponding wallet, and you have no chance of ever getting them back.
So let’s try to do it more securely.
Cryptographically strong RNG
Along with a standard RNG method, programming languages usually provide a RNG specifically designed for cryptographic operations. This method is usually much more secure, because it draws entropy straight from the operating system. The result of such RNG is much harder to reproduce. You can’t do it by knowing the time of generation or having the seed, because there is no seed. Well, at least the user doesn’t enter a seed — rather, it’s created by the program.
In Python, cryptographically strong RNG is implemented in the secrets module. Let’s modify the code above to make the private key generation secure!
That is amazing. I bet you wouldn’t be able to reproduce this, even with access to my PC. But can we go deeper?
Specialized sites
There are sites that generate random numbers for you. We will consider just two here. One is random.org, a well-known general purpose random number generator. Another one is bitaddress.org, which is designed specifically for Bitcoin private key generation.
Private Key Algorithm
Can random.org help us generate a key? Definitely, as they have service for generating random bytes. But two problems arise here. Random.org claims to be a truly random generator, but can you trust it? Can you be sure that it is indeed random? Can you be sure that the owner doesn’t record all generation results, especially ones that look like private keys? The answer is up to you. Oh, and you can’t run it locally, which is an additional problem. This method is not 100% secure.
Now, bitaddress.org is a whole different story. It’s open source, so you can see what’s under its hood. It’s client-side, so you can download it and run it locally, even without an Internet connection.
So how does it work? It uses you — yes, you — as a source of entropy. It asks you to move your mouse or press random keys. You do it long enough to make it infeasible to reproduce the results.
Are you interested to see how bitaddress.org works? For educational purposes, we will look at its code and try to reproduce it in Python.
Quick note: bitaddress.org gives you the private key in a compressed WIF format, which is close to the WIF format that we discussed before. For our purposes, we will make the algorithm return a hex string so that we can use it later for a public key generation.
Bitaddress: the specifics
Bitaddress creates the entropy in two forms: by mouse movement and by key pressure. We’ll talk about both, but we’ll focus on the key presses, as it’s hard to implement mouse tracking in the Python lib. We’ll expect the end user to type buttons until we have enough entropy, and then we’ll generate a key.
Bitaddress does three things. It initializes byte array, trying to get as much entropy as possible from your computer, it fills the array with the user input, and then it generates a private key.
Bitaddress uses the 256-byte array to store entropy. This array is rewritten in cycles, so when the array is filled for the first time, the pointer goes to zero, and the process of filling starts again.
The program initiates an array with 256 bytes from window.crypto. Then, it writes a timestamp to get an additional 4 bytes of entropy. Finally, it gets such data as the size of the screen, your time zone, information about browser plugins, your locale, and more. That gives it another 6 bytes.
After the initialization, the program continually waits for user input to rewrite initial bytes. When the user moves the cursor, the program writes the position of the cursor. When the user presses buttons, the program writes the char code of the button pressed.
Finally, bitaddress uses accumulated entropy to generate a private key. It needs to generate 32 bytes. For this task, bitaddress uses an RNG algorithm called ARC4. The program initializes ARC4 with the current time and collected entropy, then gets bytes one by one 32 times.
This is all an oversimplification of how the program works, but I hope that you get the idea. You can check out the algorithm in full detail on Github.
Doing it yourself
For our purposes, we’ll build a simpler version of bitaddress. First, we won’t collect data about the user’s machine and location. Second, we will input entropy only via text, as it’s quite challenging to continually receive mouse position with a Python script (check PyAutoGUI if you want to do that).
That brings us to the formal specification of our generator library. First, it will initialize a byte array with cryptographic RNG, then it will fill the timestamp, and finally it will fill the user-created string. After the seed pool is filled, the library will let the developer create a key. Actually, they will be able to create as many private keys as they want, all secured by the collected entropy.
Initializing the pool
Here we put some bytes from cryptographic RNG and a timestamp. __seed_int and __seed_byte are two helper methods that insert the entropy into our pool array. Notice that we use secrets.
Seeding with input
Here we first put a timestamp and then the input string, character by character.
Generating the private key
This part might look hard, but it’s actually very simple.
Algorithms For Generating Private Key West
First, we need to generate 32-byte number using our pool. Unfortunately, we can’t just create our own random object and use it only for the key generation. Instead, there is a shared object that is used by any code that is running in one script.
What does that mean for us? It means that at each moment, anywhere in the code, one simple random.seed(0) can destroy all our collected entropy. We don’t want that. Thankfully, Python provides getstate and setstate methods. So, to save our entropy each time we generate a key, we remember the state we stopped at and set it next time we want to make a key.
Second, we just make sure that our key is in range (1, CURVE_ORDER). This is a requirement for all ECDSA private keys. The CURVE_ORDER is the order of the secp256k1 curve, which is FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141.
Finally, for convenience, we convert to hex, and strip the ‘0x’ part.
In action
Let’s try to use the library. Actually, it’s really simple: you can generate a private key in three lines of code!
Algorithms For Generating Private Key Example
You can see it yourself. The key is random and totally valid. Moreover, each time you run this code, you get different results.
Conclusion
As you can see, there are a lot of ways to generate private keys. They differ in simplicity and security.
Sudoku Generating Algorithm
Generating a private key is only a first step. The next step is extracting a public key and a wallet address that you can use to receive payments. The process of generating a wallet differs for Bitcoin and Ethereum, and I plan to write two more articles on that topic.
If you want to play with the code, I published it to this Github repository.
I am making a course on cryptocurrencies here on freeCodeCamp News. The first part is a detailed description of the blockchain.
Algorithms For Generating Private Keyboard
I also post random thoughts about crypto on Twitter, so you might want to check it out.